Cartan geometry

Origins and motivation

History

Differential geometers in the late 19th and early 20th centuries were very interested in using collections of model spaces (such as planes or spheres) to describe the geometry of surfaces. A family of model spaces attached to each point of a surface $S$ is called a congruence. For example, the collection of tangent planes to a surface, or a collection of tangent spheres (one in every point of the surface). The idea, I guess, was to substitute the complicated object $S$ by a collection of simpler objects (model spaces).

A Cartan connection provides an identification between the model spaces in the congruence along any curve in $S$. An important feature of these identifications is that the point of contact of the model space with $S$ _always moves_ with the curve. This generic condition is characteristic of Cartan connections.

Generalization of manifolds with affine connections

To understand the idea of a Cartan connection, a good starting point is to analyse first the particular case of a smooth manifold with an affine connection. An affine connection on a manifold $M$ is vinculated to a principal connection $\omega$ on the frame bundle $P$ of $M$ (see here). This device let us speak about geodesics, parallel transport, and so on.

Now, let's think: what is a vector $v\in T_pP$?

The point $p\in P$ represents a point $x$ in the manifold together with a choice of a basis for $T_x M$, and $v$ represents the beginning of a curve $\alpha$ in $M$ leaving $x$ and a choice of a basis for every $T_{\alpha(t)}M$. The value of $\omega_p(v)\in \mathfrak{gl}(n)$ is an "extra data" that tells us how the basis is changing when we move along $\alpha$ . This is "not natural", and must be introduced by hand.

But observe that, in addition, the projection of $v$, the vector $d\pi_p(v)=\alpha'(0)\in T_xM$, have (tautological) coordinates $(v_1,\ldots,v_n)$ in the basis represented by $p$.

Moreover, this assignation

is linear. That is, the frame bundle has a natural $\mathbb{R}^n$-valued 1-form $\theta$ that is horizontal, in the sense that for a vertical vector $v$ we have $\theta(v)=0$. And it is right equivariant, that is,

(Think of this last expression as a coordinate change. In the left hand side we are applying the matrix $g$ to the basis elements, and in the right hand side to the coordinates of the vector).

This additional structure of the frame bundle is what is usually called a solder form. The value of $\theta_p(v)$ tells us how much are we moving in $M$ independently of the change in the basis.

The pair $(\omega,\theta)$ is the geometry of the manifold. In what sense?

Suppose I am situated in a point $x\in M$ with a choice of a basis of $T_xM$ (to do some Physics, for example). So I have chosen a point $p\in P=FM$. If I move to other configurations (point+basis) I am describing a curve $\gamma(t)$ with $\gamma(0)=p$. Suppose a small (but not infinitesimal) time $t$. Since for any $p\in P$ we have $p=point+basis$, we will denote $X(p)=point$ and $B(p)=basis$. All of this is "loosely speaking", of course. We can consider the following approximations (since $t$ is small):

• $\gamma(t) \asymp p+v$, $v\in T_p P$.

• $B(\gamma(t))\asymp B(p)+\omega_p(v)$. Observe that, in some sense, $B(p)\in GL(n)$ and $\omega_p(v)\in \mathfrak{gl}(n)$, so it would be something like $B(p)+\omega_p(v)\approx B(p) e^{t\omega_p(v)}$...

• $X(\gamma(t))=X(p)+\theta_p(v)$. So $\theta_p(v)$ is a kind of translation [^1].

What we are doing here is to treat $M$ and their "configurations" as if after zooming it on $p$ it behaves like $\mathbb{R}^n$ seen as the quotient $Aff(n)/GL(n)$. The construction above let us formalize these approximations.

Finally, observe that the pair $\eta=(\omega,\theta)$ (the principal connection and the solder form) defines a 1-form $\eta$ on $P$, with values in the Lie algebra $\mathfrak {g}$ of the semidirect product $G=\mathbb{R}^n \rtimes H$, which provides us with an isomorphism of each tangent space $T_pP$ with $\mathfrak{g}$. It induces a principal connection α on the associated principal $G$-bundle $P \times_{H} G$. This is what is called a Cartan connection.

The trivialization of $TP$ achieved in this way

provides an absolute parallelism of $P$ or, in other words, a parallelization of $P$.

Generalization of Riemannian manifolds

Important: see this section first.

There are two kind of Cartan geometries related to the classical point of view of pseudo-Riemannian manifolds. They are Euclidean geometrys and Riemannian geometrys.

Given a Riemannian geometry on $M$, it determines a (pseudo)-Riemannian metric on $M$ up to constant scale factor (see @sharpe2000differential Proposition 3.2 page 238).

Conversely, given a pseudo-Riemannian manifold $(M,g)$ there is exactly one Riemannian geometry whose associated metric is, up to scale, the original $g$ (Theorem 3.5 in @sharpe2000differential).

Idea of the converse:

A pseudo-Riemannian manifold has a "natural" torsion-free connection, the Levi-Civita connection. As it is said above, a linear connection on a manifold induces a principal connection on the frame bundle and, together with the solder form, a Cartan geometry. But in this particular case this linear connection also defines a principal connection on the orthonormal frame bundle (see condition 1 in Levi-Civita connection). And because of condition 2 in Levi-Civita connection this Cartan geometry is torsion-free. In conclusion: a Riemannian manifold induces a Riemannian geometry.

Generalization of G-structures

The idea of G-structure is a generalization of the construction above. If we take a general subgroup $G$ of $GL(n)$ instead of $O(n)$ we get a $G$-structure on $M$ and if we again add a connection $\omega$ we obtain a Cartan geometry on $M$ modelled on $(\mathbb{R}^n \rtimes G,G)$ with Cartan connection given by $(\omega,\theta)$, begin $\theta$ the solder form. See also G-structure#Relation to Cartan geometries.

I think every G-structure on a manifold $M$ is a Cartan geometry modelled on $(\mathbb{R}^n \rtimes G,G)$.

Generalization of Klein geometries

A Klein geometry $(G,H)$ can be seen like an $H$-principal bundle (with $P=G)$. Let's call $\eta$ to the Maurer-Cartan form of $G$ , and $\eta_H$ to the Maurer-Cartan form of the principal bundle $G\to G/H$. They satisfy special properties:

1. For every $h\in H$, $R_h^*\eta_H=Ad_{h^{-1}}\eta_H$.

2. $\eta_H$ is the inverse of the map

3. For $g\in P$, $\eta_g|_{VgP}=(\eta_H)_g$.

4. For $g\in P$, $\eta_g$ is a linear isomorphism $T_gP \to \mathfrak{g}$, and so it defines a trivialization of $TP$ (that is, $P$ is a parallelizable manifold, or equivalently, it has a absolute parallelism).

5. $d\eta+\frac{1}{2}[\eta,\eta]=0$ (Maurer-Cartan form#Structural equation).

Observe that in a general $H$-principal bundle $P$ the Maurer-Cartan form $\theta^P$ satisfies 1. and 2. If we manage to find a group $G$ and 1-form $\eta$ in $P$ that restrict to $\theta^P$ and that satisfies 3. we have a Cartan geometry. Observe that $P$ is not necessarily equal to $G$, but has the same dimension. Condition 5 do not need to be satisfied and the output is called the curvature.

Wikipedia Cartan Geometries

Definition and remarks

[Wise 2009]

A Cartan geometry modeled on the Klein geometry $(G,H)$ is a $H$-principal bundle

equipped with a $\mathfrak{g}$-valued 1-form $A$ on $P$ called the Cartan connection and satisfying

1. For every $p\in P$,

is a linear isomorphism.

2. For every $h\in H$, $R_h^*A=Ad_{h^{-1}}A$.

3. For every $p\in P$, the restriction of $A_p$ to the subspace $V_pP\subseteq T_pP$ coincides with the Maurer-Cartan form of the H-bundle. So it takes values on $\mathfrak{h}\subseteq \mathfrak{g}$.

We highlight the following remarks:

• The Cartan connection is an extension of the Maurer-Cartan form of $P$ which takes values in a bigger Lie algebra $\mathfrak{g}$. The usual principal connection on a principal bundle is also an extension but take values in $\mathfrak{h}$.

• The group $G$ must have the same dimension than the manifold $P$. In other words, $G/H$ must have the same dimension than $M$.

• In the same way that the inverse at every point of the Maurer-Cartan form of $P$ (the so denoted $i_p$) give rise to a vertical vector field associated to every $v\in \mathfrak{h}$, the inverse at every point of $A_p$ gives us an injection

If $v\in \mathfrak{h}$ we obtain a vertical vector field; if not, it yields a vector field transverse to the fibres.

• In a Klein geometry the Maurer-Cartan form satisfies the structural equation, but this is not the case for a Cartan geometry. This fail is called the curvature of a Cartan geometry.

• Contrary to Klein geometrys, Cartan geometries no longer have a well-defined action of G on them. However, a Cartan connection supplies a way of connecting the infinitesimal model spaces within the manifold by means of parallel transport. (I have to see how, yet).

Important case: reductive Cartan geometry.

Curvature

See curvature of a Cartan geometry

Torsion

See torsion of a Cartan geometry

Example: hamster in a ball

[Wise 2009]

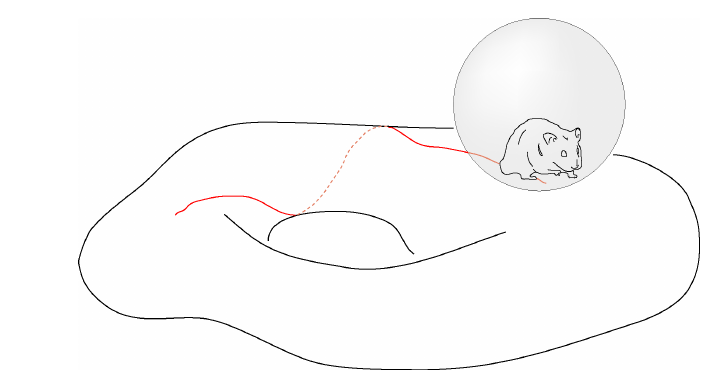
Consider a manifold $M$, explored by a hamster inside a ball. For the hamster, there is a group of posible movements: $G=SO(3)$ but some of them do not let it to change the point of $M$ where it stands: the rotations over itself $H=SO(2)$. This is the Klein geometry $(G,H)$ used to model the manifold.

What would be $P$ in this context? It would be a $SO(2)$-principal bundle over $M$ representing the set of posible "hamster configurations", that is, combinations of "positions-orientations" of the hamster.

And what about the Cartan connection $A$? For every configuration $p\in P$ we can consider "infinitesimal changes", that is, vectors leaving $p$, for example $v\in T_pP$. This change could be only a change of "orientation", but not of position. And this would mean that $v$ is a vertical vector and

An infinitesimal change $v$ that implies a change of position would have an image

The maps $A_p$ must be isomorphisms in order to exist a total correspondence between changes in $S^2=G/H$ (the world as perceived by the hamster) and changes in $P$.

Example: An explorer of th 15th century

Consider a person standing on a flat planar 'model Earth', tangent to the actual spherical Earth. The plane rolls as he walks. This rolling gives a $E(2)/SO(2)$ Cartan geometry of the Earth's surface. He could use the rolling motion to try drawing a local map of the Earth on the plane

[^1]: Do we have a kind of exponential map here similar to the previous point? Or in other words: if we choose a direction $\widetilde{v}=\theta_p(v)$ in $M$ is there a "canonical" point $y\in M$ to which do we arrive after moving during a time $t$? I don't think so, unless the whole $P$ is a group (in this case it would be $\mathbb{R}^n\rtimes GL(n)$). Although, on the other hand, we have the notion of geodesic. So we could move along the geodesic with direction given by $\widetilde{v}$.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es